REPASO DE CONCEPTOS PREVIOS ESTADISTICOS PARA ANALISIS DE CONFIABILIDAD

 Traducción de reliawiki.org

Esta sección proporciona una breve introducción elemental a las ecuaciones y definiciones estadísticas más comunes y fundamentales utilizadas en la ingeniería de confiabilidad y el análisis de datos de vida.

Variables aleatorias

En general, la mayoría de los problemas en la ingeniería de confiabilidad tratan con medidas cuantitativas, como el tiempo hasta la falla de un componente, o medidas cualitativas, como si un componente es defectuoso o no defectuoso. Entonces podemos usar una variable aleatoria X para denotar estas posibles medidas.

En el caso de los tiempos de falla, nuestra variable aleatoria X es el tiempo de fallo del componente y puede tomar una infinidad de valores posibles en un rango de 0 a infinito (ya que no sabemos el tiempo exacto a priori ). Nuestro componente puede fallar en cualquier momento después del tiempo 0 (por ejemplo, a las 12 horas o a las 100 horas y así sucesivamente), por lo tanto X puede tomar cualquier valor en este rango. En este caso, nuestra variable aleatoria X se dice que es una variable aleatoria continua . En esta referencia, trataremos casi exclusivamente con variables aleatorias continuas.

Al juzgar que un componente es defectuoso o no defectuoso, solo son posibles dos resultados. Es decir, X es una variable aleatoria que puede tomar uno de solo dos valores (digamos defectuoso = 0 y no defectuoso = 1). En este caso, se dice que la variable es una variable aleatoria discreta.

La función de densidad de probabilidad y la función de distribución acumulativa

La función de densidad de probabilidad ( pdf ) y la función de distribución acumulativa ( cdf ) son dos de las funciones estadísticas más importantes en confiabilidad y están muy estrechamente relacionadas. Cuando se conocen estas funciones, se puede derivar u obtener casi cualquier otra medida de confiabilidad de interés. Ahora veremos más de cerca estas funciones y cómo se relacionan con otras medidas de confiabilidad, como la función de confiabilidad y la tasa de fallas.

De probabilidad y estadística, dada una variable aleatoria continua x , denotamos:

• La función de densidad de probabilidad, pdf , como f ( x ) .

• La función de distribución acumulada, cdf , como F ( x ) .

El pdf y cdf dan una descripción completa de la distribución de probabilidad de una variable aleatoria. La siguiente figura ilustra un pdf .

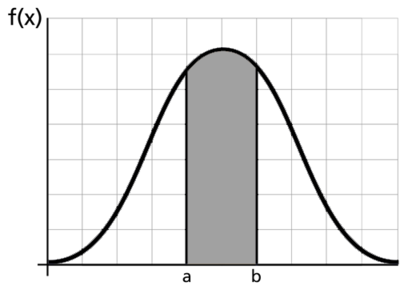
Las siguientes figuras ilustran la pdf - cdf .

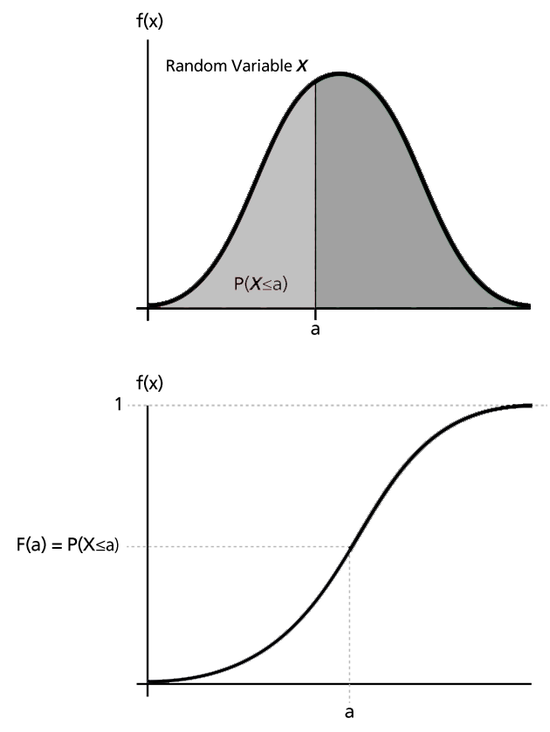
Si X es una variable aleatoria continua, entonces la función probabilidad de X es una función, f ( x ) , tal que para dos números cualesquiera, un y b con a ≤ b  :

PAGS ( un ≤ X ≤ segundo ) = ∫ segundo un F ( X ) re X  

Es decir, la probabilidad de que X toma un valor en el intervalo [ un , b ] es el área bajo la función de densidad de un para b , como se muestra arriba. El pdf representa la frecuencia relativa de los tiempos de falla en función del tiempo.

La cdf es una función, F ( x ) , de una variable aleatoria X , y se define para un número X por:

F ( X ) = PAGS ( X ≤ X ) = ∫ X 0 F ( s ) re s  

Es decir, para un número X , F ( x ) es la probabilidad de que el valor observado de X será como máximo X . El cdf representa los valores acumulados del pdf . Es decir, el valor de un punto en la curva de la cdf representa el área bajo la curva a la izquierda de ese punto en la pdf . En confiabilidad, la cdf se utiliza para medir la probabilidad de que el elemento en cuestión falle antes del valor de tiempo asociado, t , y también se denomina fiabilidad .

Tenga en cuenta que dependiendo de la función de densidad, denotada por f ( x ) , los límites variarán según la región sobre la que se defina la distribución. Por ejemplo, para las distribuciones de vida consideradas en esta referencia, a excepción de la distribución normal, este rango sería [ 0 , + ∞ ] .

Relación matemática: pdf y cdf

La relación matemática entre el pdf y cdf viene dada por:

F ( X ) = ∫ X 0 F ( s ) re s

donde s es una variable ficticia de integración.

En cambio:

F ( X ) = re ( F ( X ) ) re X

La cdf es el área bajo la función de densidad de probabilidad hasta un valor de X . El área total bajo el pdf siempre es igual a 1, o matemáticamente:

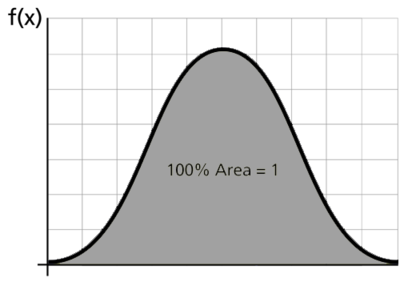
∫ + ∞ − ∞ F ( X ) re X = 1

La conocida distribución normal (o gaussiana) es un ejemplo de función de densidad de probabilidad. El pdf para esta distribución está dado por:

F ( t ) = 1 σ 2 π √ mi - 1 2 ( t - μ σ ) 2

donde m es la media y σ es la desviación estándar. La distribución normal tiene dos parámetros, m y σ .

Otra es la distribución lognormal, cuya pdf viene dada por:

F ( t ) = 1 t ⋅ σ ′ 2 π √ mi - 1 2 ( t ′ - μ ′ σ ′ ) 2

donde μ ' es la media de los logaritmos naturales de los tiempos hasta la falla y σ ′ es la desviación estándar de los logaritmos naturales de los tiempos de falla. Nuevamente, esta es una distribución de 2 parámetros.

Función de confiabilidad

La función de confiabilidad se puede derivar usando la definición anterior de la función de distribución acumulada, F ( X ) = ∫ X 0 F ( s ) re s . De nuestra definición de cdf , la probabilidad de que ocurra un evento por tiempo t es dado por:

F ( t ) = ∫ t 0 F ( s ) re s  

O bien, se podría equiparar este evento a la probabilidad de que una unidad falle por tiempo t .

Dado que esta función define la probabilidad de falla en un cierto tiempo, podríamos considerarla como la función de falta de confiabilidad. Restar esta probabilidad de 1 nos dará la función de confiabilidad, una de las funciones más importantes en el análisis de datos de vida. La función de fiabilidad da la probabilidad de éxito de una unidad que emprende una misión de una duración determinada. La siguiente figura ilustra esto.

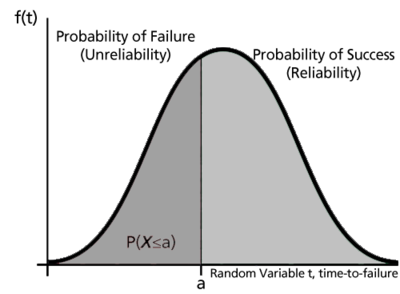
Para mostrar esto matemáticamente, primero definimos la función de falta de confiabilidad, q ( t ) , que es la probabilidad de falla, o la probabilidad de que nuestro tiempo hasta la falla esté en la región de 0 y t . Esto es lo mismo que el cdf . entonces desde F ( t ) = ∫ t 0 F ( s ) re s  :

Q ( t ) = F ( t ) = ∫ t 0 F ( s ) re s

La confiabilidad y la falta de confiabilidad son los dos únicos eventos que se consideran y se excluyen mutuamente; por tanto, la suma de estas probabilidades es igual a la unidad.

Entonces:

Q ( t ) + R ( t ) = R ( t ) = R ( t ) = R ( t ) = 1 1 − Q ( t ) 1 − ∫ t 0 F ( s ) re s ∫ ∞ t F ( s ) ds _

En cambio:

F ( t ) = - re ( R ( t ) ) re t

Función de confiabilidad condicional

La confiabilidad condicional es la probabilidad de completar con éxito otra misión luego de completar con éxito una misión anterior. Para los cálculos de fiabilidad condicional se debe tener en cuenta el tiempo de la misión anterior y el tiempo de la misión a realizar. La función de confiabilidad condicional viene dada por:

R ( T | T ) = R ( T + T ) R ( T )  

Función de tasa de fallas

La función de tasa de fallas permite determinar el número de fallas que ocurren por unidad de tiempo. Omitiendo la derivación, la tasa de fallas se da matemáticamente como:

λ ( t ) = F ( t ) R ( t )  

Esto da la tasa de falla instantánea, también conocida como función de riesgo. Es útil para caracterizar el comportamiento de falla de un componente, determinar la asignación del equipo de mantenimiento, planificar el aprovisionamiento de repuestos, etc. La tasa de falla se indica como fallas por unidad de tiempo.

Vida media (MTTF)

La función de vida media, que proporciona una medida del tiempo medio de funcionamiento hasta el fallo, está dada por:

T ¯ ¯ ¯ ¯ = metro = ∫ ∞ 0 t ⋅ F ( t ) re t

Este es el tiempo esperado o promedio hasta la falla y se denota como MTTF (Mean Time To Failure).

El MTTF, a pesar de ser un índice de rendimiento de confiabilidad, no brinda información sobre la distribución de fallas del componente en cuestión cuando se trata de la mayoría de las distribuciones de vida útil. Debido a que distribuciones muy diferentes pueden tener medios idénticos, no es aconsejable utilizar el MTTF como la única medida de la confiabilidad de un componente.

Vida media

vida media, T ~ , es el valor de la variable aleatoria que tiene exactamente la mitad del área bajo el pdf a su izquierda y la otra mitad a su derecha. Representa el centroide de la distribución. La mediana se obtiene resolviendo la siguiente ecuación para T ˘ . (Para datos individuales, la mediana es el valor del punto medio).

∫ T ˘ − ∞ F ( t ) re t = 0,5  

Vida modal (o modo)

La vida modal (o modo), T ~ , es el valor de T que satisface:

re [ F ( t ) ] re t = 0  

Para una distribución continua, la moda es el valor de t que corresponde a la máxima densidad de probabilidad (el valor en el que el pdf tiene su valor máximo, o el pico de la curva).

Distribuciones de por vida

Una distribución estadística se describe completamente por su pdf . En las secciones anteriores, usamos la definición de pdf para mostrar cómo se pueden derivar todas las demás funciones más comúnmente utilizadas en ingeniería de confiabilidad y análisis de datos de vida. La función de confiabilidad, la función de tasa de fallas, la función de tiempo medio y la función de vida media se pueden determinar directamente a partir de la pdf , o f ( t ) . Existen diferentes distribuciones, como la normal (Gaussiana), exponencial, Weibull, etc., y cada una tiene una forma predefinida de f ( t ) que se puede encontrar en muchas referencias. De hecho, existen ciertas referencias que se dedican exclusivamente a diferentes tipos de distribuciones estadísticas. Estas distribuciones fueron formuladas por estadísticos, matemáticos e ingenieros para modelar matemáticamente o representar cierto comportamiento. Por ejemplo, la distribución de Weibull fue formulada por Waloddi Weibull y por eso lleva su nombre. Algunas distribuciones tienden a representar mejor los datos de vida y se denominan más comúnmente "distribuciones de vida".

Una introducción más detallada a este tema se presenta en Life Distributions .