ESTIMACION DE PARAMETROS DE VIDA PARA ANALISIS DE CONFIABILIDAD

 ESTIMACION DE PARAMETROS

El término estimación de parámetros se refiere al proceso de usar datos de muestra (en ingeniería de confiabilidad, por lo general datos de tiempos de falla o éxito) para estimar los parámetros de la distribución seleccionada. Hay varios métodos de estimación de parámetros disponibles. Esta sección presenta una descripción general de los métodos disponibles utilizados en el análisis de datos de vida. Más específicamente, comenzamos con el método relativamente simple de Trazado de Probabilidad y continuamos con los métodos más sofisticados de Regresión de Rango (o Mínimos Cuadrados), Estimación de Máxima Verosimilitud y Métodos de Estimación Bayesiana.

Trazado de probabilidad

El método menos intensivo desde el punto de vista matemático para la estimación de parámetros es el método de trazado de probabilidades. Como implica el término, el trazado de probabilidad implica un trazado físico de los datos en un papel de trazado de probabilidad . Este método se implementa fácilmente a mano, dado que uno puede obtener el papel de trazado de probabilidad apropiado.

El método de representación gráfica de probabilidad toma la CDF de la distribución e intenta linealizarla empleando un papel especialmente construido. Las siguientes secciones ilustran los pasos de este método usando la distribución de Weibull de 2 parámetros como ejemplo. Esto incluye:

• Linealizar la función de falta de fiabilidad
• Construya el papel de trazado de probabilidad
• Determinar las posiciones X e Y de los puntos de la trama

Y luego usar la gráfica para leer cualquier tiempo en particular o valor de interés de confiabilidad/falta de confiabilidad.

Linealización de la función de falta de fiabilidad

En el caso del Weibull de 2 parámetros, la cdf (también la falta de confiabilidad q ( t ) ) es dado por:

F ( t ) = Q ( t ) = 1 - mi - ( t η ) β

Luego, esta función puede linealizarse (es decir, ponerse en la forma común de y = metro ′ x + segundo formato) de la siguiente manera :

Q ( t ) = ln ( 1 - Q ( t ) ) = ln ( 1 - Q ( t ) ) = ln ( - ln ( 1 - Q ( t ) ) ) = ln ( ln ( 1 1 - Q ( t ) ) ) = 1 - mi - ( t η ) β ln [ mi - ( t η ) β ] - ( t η ) β β ( ln ( t η ) ) β ln t - β ln η

Luego, configurando:

y = en ( en ( 1 1 − Q ( t ) ) )

y:

x = ln ( t )

la ecuación se puede reescribir como:

y = β x - β ln ( η )

que ahora es una ecuación lineal con una pendiente de:

m = β

y un intercepto de:

segundo = - β ⋅ l norte ( η )

Construyendo el papel

La siguiente tarea es construir el papel de trazado de probabilidad de Weibull con los ejes y y x apropiados. La transformación del eje x es simplemente logarítmica. El eje y es un poco más complejo y requiere una transformación recíproca logarítmica doble, o:

y = en ( en ( 1 1 − Q ( t ) ) ) )

donde q ( t ) es la falta de fiabilidad.

Dichos documentos han sido creados por diferentes proveedores y se denominan documentos de trazado de probabilidad . El sitio web de recursos de ingeniería de confiabilidad de ReliaSoft en www.weibull.com tiene diferentes papeles de trazado disponibles para descargar .

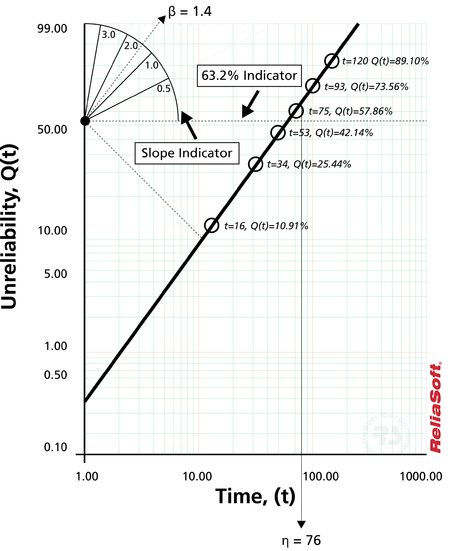
Para ilustrar, considere la siguiente gráfica de probabilidad en un tipo ligeramente diferente de papel de probabilidad de Weibull.

Este documento está construido en base a las transformaciones y y x mencionadas, donde el eje y representa la falta de confiabilidad y el eje x representa el tiempo. Ambos valores deben conocerse para cada punto de tiempo hasta la falla que queramos graficar.

Entonces, dada la y yx X valor para cada punto, los puntos se pueden poner fácilmente en la gráfica. Una vez que se han colocado los puntos en el gráfico, se dibuja la mejor línea recta posible a través de estos puntos. Una vez que se ha dibujado la línea, se puede obtener la pendiente de la línea (algunos documentos de probabilidad incluyen un indicador de pendiente para simplificar este cálculo). Este es el parámetro b , que es el valor de la pendiente. Para determinar el parámetro de escala, la (también llamada vida característica ), se lee el tiempo en el eje x correspondiente a Q ( t ) = 63,2 .

Tenga en cuenta que en:

Q ( t = η ) = = = = 1 - 0.632 - ( t η ) β 1 - mi - 1 mi 63.2

Por lo tanto, si ingresamos al y eje Q ( t ) = 63,2 , el valor correspondiente de t será igual a la . Así, utilizando esta sencilla metodología, se pueden estimar los parámetros de la distribución de Weibull.

Determinación de la posición X e Y de los puntos del gráfico

Los puntos en el gráfico representan nuestros datos o, más específicamente, nuestros datos de tiempos de falla. Si, por ejemplo, probamos cuatro unidades que fallaron a las 10, 20, 30 y 40 horas, entonces usaríamos estos tiempos como nuestros x o valores de tiempo.

Determinar las y , o los valores de falta de fiabilidad, es un poco más complejo. Para determinar las y , primero debemos determinar un valor que indique la falta de confiabilidad correspondiente para esa falla. En otras palabras, necesitamos obtener el porcentaje acumulado de fallas para cada tiempo hasta la falla. Por ejemplo, el porcentaje acumulativo de errores a las 10 horas puede ser del 25 %, a las 20 horas del 50 %, y así sucesivamente. Este es un método simple que ilustra la idea. El problema con este método simple es el hecho de que el punto del 100% no está definido en la mayoría de las gráficas de probabilidad; por lo tanto, se debe utilizar un enfoque alternativo y más sólido. El método más utilizado para determinar este valor es el método de obtención del rango medio para cada falla, como se analiza a continuación.

rangos medios

El método de rangos medianos se usa para obtener una estimación de la falta de confiabilidad para cada falla. El rango medio es el valor que la verdadera probabilidad de falla, Q ( T j ) , debe tener en j t h falla de una muestra de norte unidades al 50% de nivel de confianza.

El rango se puede encontrar para cualquier punto porcentual, PAG , mayor que cero y menor que uno, resolviendo la ecuación binomial acumulativa para DESDE . Esto representa el rango, o estimación de falta de confiabilidad, para el j t h falla en la siguiente ecuación para el binomio acumulativo:

PAGS = ∑ norte k = j ( norte k ) Z k ( 1 - Z ) norte - k

donde norte es el tamaño de la muestra y j el número de pedido.

El rango medio se obtiene resolviendo esta ecuación para DESDE en P = 0,50 :

0,50 = ∑ norte k = j ( norte k ) Z k ( 1 - Z ) norte - k

Por ejemplo, si norte = 4 y tenemos cuatro fallas, resolveríamos la ecuación de rango mediano para el valor de DESDE cuatro veces; una vez por cada falla con j = 1 , 2 , 3 y 4 . Este resultado se puede usar como estimación de la falta de confiabilidad para cada falla o el y posición de trazado. (Consulte también La distribución de Weibull para ver un ejemplo paso a paso de este método). La solución de la ecuación binomial acumulativa para DESDE requiere el uso de métodos numéricos.

Enfoque de distribuciones Beta y F

Un método más directo y fácil de estimar los rangos medianos es aplicar dos transformaciones a la ecuación binomial acumulativa, primero a la distribución beta y luego a la distribución F, lo que da como resultado [12, 13] :

METRO R metro norte = = = 1 1 + norte - j + 1 j F 0,50 ; metro ; norte 2 ( norte - j + 1 ) 2 j

donde F0,50 _ ; metro ; norte denota la F distribución en el punto 0,50, con metro y norte grados de libertad, por falla j de norte unidades.

Aproximación de Benard para rangos medianos

Otra aproximación rápida y menos precisa de los rangos medianos también viene dada por:

METRO R = j − 0,3 norte + 0,4

Esta aproximación de los rangos medianos también se conoce como aproximación de Benard .

Kaplan Meier

El estimador de Kaplan-Meier (también conocido como estimador del límite del producto ) se usa como una alternativa al método de rangos medianos para calcular las estimaciones de la falta de confiabilidad con fines de representación gráfica de probabilidad. La ecuación del estimador viene dada por:

F ˆˆ ( t yo ) = 1 - ∏ yo j = 1 r j - norte j norte j ,  yo = 1 ,. _ . . , metro

donde:

m = n = n i = r j = s j = número total de puntos de datos el número total de unidades n − ∑ j = 0 i − 1 s j − ∑ j = 0 i − 1 r j , i = 1,. ..,m número de fallas en el jth jth grupo y número de unidades supervivientes en el datos , de grupo

Ejemplo de gráfico de probabilidad

Esta misma metodología se puede aplicar a otras distribuciones con cdf que se pueden linealizar. Existen diferentes documentos de probabilidad para cada distribución, porque diferentes distribuciones tienen diferentes CDF ecuaciones Las herramientas de software de ReliaSoft crean automáticamente estos gráficos para usted. Las escalas especiales de estos gráficos le permiten derivar las estimaciones de los parámetros directamente de los gráficos, de forma similar a b y la se obtuvieron de la gráfica de probabilidad de Weibull. El siguiente ejemplo demuestra el método nuevamente, esta vez usando la distribución exponencial de 1 parámetro.

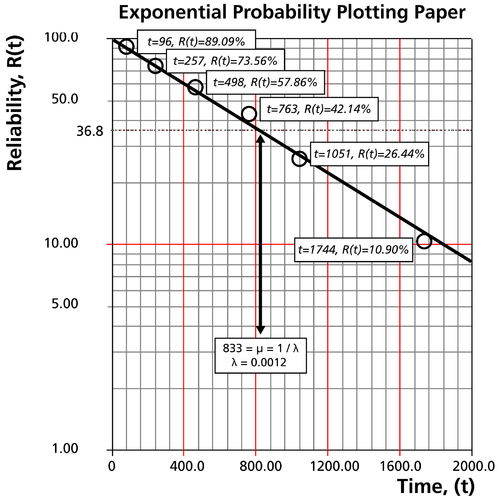
Supongamos que se prueba la confiabilidad de seis unidades idénticas en la misma aplicación y operación niveles de estres. Todas estas unidades fallan durante la prueba después de operar durante los siguientes tiempos (en horas): 96, 257, 498, 763, 1051 y 1744.

Los pasos para usar el método de representación gráfica de probabilidad para determinar los parámetros de la función de densidad de probabilidad exponencial que representa la los datos son los siguientes:

Clasifique los tiempos de falla en orden ascendente como se muestra a continuación.

falla (h) 96 257 498 763 1,051 1,744 Número de orden de falla de un tamaño de muestra de 6 1 2 3 4 5 6

Obtenga sus posiciones de trazado de rango medio. Las posiciones de clasificación mediana se utilizan en lugar de otros métodos de clasificación porque las clasificaciones medianas están en un nivel de confianza específico (50%).

Los tiempos de falla, con sus correspondientes rangos medios, se muestran a continuación:

falla (Hr) 257 498 763 1,051 1,744 mediano Rango 96 26 .44 42 .14 57 .86 73 .56 89 .10 10 .91

En un papel de probabilidad exponencial, grafique los tiempos en el eje x y sus correspondientes valor de rango en el eje y. La siguiente figura muestra un ejemplo de un artículo de probabilidad exponencial. Él el papel es simplemente un papel log-lineal.

Dibuja la mejor recta posible que pase por t = 0 y ( t ) = 100 punto y a través de los puntos graficados (como se muestra en el diagrama a continuación).

En Q ( t ) = 63,2 o R ( t ) = 36,8 punto de ordenadas, dibuja un línea recta horizontal hasta que esta línea se cruza con la línea recta ajustada. Dibuja una línea vertical a través de esta intersección hasta que cruce la abscisa. El valor en la intersección de la abscisa es la estimación de la media. Para este caso, µˆ ˆ= 833 horas lo que significa que λ = 1 μ = 0,0012 (Esto siempre es del 63,2 % porque ( T ) = 1 - 0,632 - μ μ = 1 - mi - 1 = mi = 63,2 .

Ahora cualquier valor de confiabilidad para cualquier tiempo de misión t Puede ser obtenido. por ejemplo, el la confiabilidad para una misión de 15 horas, o cualquier otro tiempo, ahora se puede obtener ya sea de forma gráfica o analítica.

Para obtener el valor del gráfico, dibuje una línea vertical desde la abscisa, en t = 15 horas, a la línea ajustada. Trace una línea horizontal desde esta intersección hasta la ordenada y lea R ( t ) . En este caso, R ( t = 15 ) = 98.15 . Esto también se puede obtener analíticamente, a partir de la función de fiabilidad exponencial.

Comentarios sobre el método de representación gráfica de probabilidad

Además del inconveniente más obvio del trazado de probabilidades, que es la cantidad de esfuerzo necesario, el trazado manual de probabilidades no siempre es consistente en los resultados. Dos personas que trazan una línea recta a través de un conjunto de puntos no siempre dibujarán esta línea de la misma manera y, por lo tanto, obtendrán resultados ligeramente diferentes. Este método se usó principalmente antes del uso generalizado de computadoras que podían realizar fácilmente los cálculos para métodos de estimación de parámetros más complicados, como los métodos de mínimos cuadrados y máxima verosimilitud.

Mínimos cuadrados (regresión de rango)

Utilizando la idea del gráfico de probabilidad, el análisis de regresión ajusta matemáticamente la mejor línea recta a un conjunto de puntos, en un intento de estimar los parámetros. Esencialmente, esta es una versión basada matemáticamente del método de trazado de probabilidad discutido anteriormente.

El método de mínimos cuadrados lineales se utiliza para todos los análisis de regresión realizados por Weibull++, excepto para los casos de las distribuciones Weibull de 3 parámetros, Weibull mixta, gamma y gamma generalizada, donde se emplea una técnica de regresión no lineal. Los términos regresión lineal y mínimos cuadrados se usan como sinónimos en esta referencia. En Weibull++, el término regresión de rango se usa en lugar de mínimos cuadrados o regresión lineal, porque la regresión se realiza en los valores de rango, más específicamente, los valores de rango mediano (representados en el eje y). El método de los mínimos cuadrados requiere que se ajuste una línea recta a un conjunto de puntos de datos, de modo que se minimice la suma de los cuadrados de la distancia de los puntos a la línea ajustada. 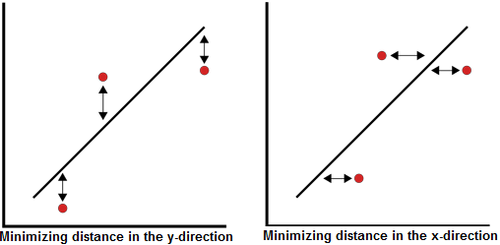Esta minimización se puede realizar en dirección vertical u horizontal. Si la regresión es sobre X , luego la línea se ajusta de modo que las desviaciones horizontales de los puntos a la línea se minimicen. Si la regresión está en Y, esto significa que la distancia de las desviaciones verticales de los puntos a la línea se minimiza. Esto se ilustra en la siguiente figura.

Regresión de rango en Y

Suponga que un conjunto de pares de datos ( x 1 , y 1 ) , ( x 2 , y 2 ) ,..., ( x norte , y norte ) fueron obtenidas y graficadas, y que X -Los valores se conocen con exactitud. Entonces, según el principio de los mínimos cuadrados, que minimiza la distancia vertical entre los puntos de datos y la línea recta ajustada a los datos, la línea recta que mejor se ajusta a estos datos es la línea recta y = a ^ + b ^ x (donde el recientemente introducido ( ^ ) indica que este valor es una estimación) tal que:

∑ yo = 1 norte ( un ^ + segundo ^ X yo - y yo ) 2 = min ∑ yo = 1 norte ( un + segundo X yo - y yo ) 2

y donde un ^ y b ^ son las estimaciones de mínimos cuadrados de un yb b , y norte es el número de puntos de datos. Estas ecuaciones se minimizan mediante estimaciones de aun y bb tal que:

un ^ = ∑ norte yo = 1 y yo norte - segundo ^ ∑ norte yo = 1 X yo norte = y ¯ - segundo ^ X ¯

y:

segundo ^ = ∑ norte yo = 1 X yo y yo - ∑ norte yo = 1 X yo ∑ norte yo = 1 y yo norte ∑ norte yo = 1 X 2 yo - ( ∑ norte yo = 1 X yo ) 2 norte

Regresión de rango en X

Suponga que un conjunto de pares de datos .., ( x 2 , y 2 ) ,..., ( x norte , y norte ) se obtuvieron y graficaron, y que los valores de y se conocen exactamente. Se aplica el mismo principio de mínimos cuadrados, pero esta vez minimizando la distancia horizontal entre los puntos de datos y la línea recta ajustada a los datos. La línea recta que mejor se ajusta a estos datos es la línea recta x = a ˆˆ + b ˆˆ y tal que:

∑ norte yo = 1 ( un ˆˆ + segundo ˆˆ y yo − X _ ) 2 = min un _ ( _ , ∑ ) segundo norte yo = 1 ( un + segundo ˆ y yo − X _ ) _

De nuevo, aun y bb son las estimaciones por mínimos cuadrados de y b , y norte es el número de puntos de datos. Estas ecuaciones se minimizan mediante estimaciones de aun y bb tal que:

un ^ = ∑ norte yo = 1 X yo norte - segundo ^ ∑ norte yo = 1 y yo norte = X ¯ - segundo ^ y ¯

y:

segundo ˆˆ = ∑ norte yo = 1 X yo y yo - ∑ norte yo = 1 X yo ∑ norte yo = 1 y yo norte ∑ norte yo = 1 y 2 yo - ( ∑ norte yo = 1 y yo ) 2 norte

Las relaciones correspondientes para determinar los parámetros para distribuciones específicas (es decir, Weibull, exponencial, etc.) se presentan en los capítulos que cubren esa distribución.

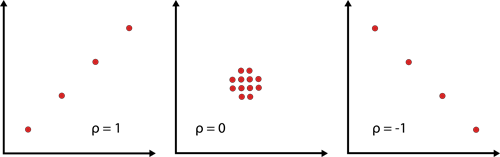
Coeficiente de correlación

El coeficiente de correlación es una medida de qué tan bien se ajusta el modelo de regresión lineal a los datos y generalmente se denota por ρ . En el caso del análisis de datos de vida, es una medida de la fuerza de la relación lineal (correlación) entre los rangos medianos y los datos. El coeficiente de correlación de la población se define de la siguiente manera:

ρ = σ x y σ x σ y

donde σ x y = covarianza de X y y , x _ = desviación estándar de X , y y _ = desviación estándar de y .

El estimador de ρ es el coeficiente de correlación de la muestra, ρ ^ , dada por:

ρ ^ = ∑ norte yo = 1 X yo y yo - ∑ norte yo = 1 X yo ∑ norte yo = 1 y yo norte ⎛ ⎝ ⎜ ⎜ ∑ norte yo = 1 x 2 yo - ( 1 norte yo = yo X yo ) 2 norte ⎞ ⎠ ⎛ ⎟ ⎜ ⎟ ⎜ ∑ ∑ norte yo = 1 y 2 yo - ( 1 norte yo = yo y yo ) 2 norte ⎞ ⎠ ⎟ ⎟       

El rango de ρ ^ es − 1 ≤ ρ ^ ≤ 1 .

Cuanto más cerca esté el valor de ± 1 , mejor será el ajuste lineal. Tenga en cuenta que +1 indica un ajuste perfecto (los valores emparejados ( x yo , y yo ) se encuentran en línea recta) con pendiente positiva, mientras que -1 indica un ajuste perfecto con pendiente negativa. Un valor de coeficiente de correlación de cero indicaría que los datos están dispersos aleatoriamente y no tienen patrón ni correlación en relación con el modelo de línea de regresión.

Comentarios sobre el método de los mínimos cuadrados

El método de estimación de mínimos cuadrados es bastante bueno para funciones que se pueden linealizar. Para estas distribuciones, los cálculos son relativamente fáciles y directos, con soluciones de forma cerrada que pueden dar una respuesta fácilmente sin tener que recurrir a técnicas numéricas o tablas. Además, esta técnica proporciona una buena medida de la bondad de ajuste de la distribución elegida en el coeficiente de correlación. Los mínimos cuadrados generalmente se usan mejor con conjuntos de datos que contienen datos completos, es decir, datos que consisten solo en tiempos únicos de falla sin datos censurados o de intervalo. (Consulte Clasificación de datos de vida para obtener información sobre los diferentes tipos de datos, incluidos datos completos, censurados por la izquierda, censurados por la derecha (o suspendidos) y de intervalo).

Ver también:

• Ecuaciones de regresión de mínimos cuadrados/rango
• Análisis de datos agrupados

Métodos de clasificación para datos censurados

Todos los datos disponibles deben ser considerados en el análisis de los datos de tiempo hasta la falla. Esto incluye el caso cuando una unidad particular en una muestra ha sido removida de la prueba antes de fallar. Un elemento, o unidad, que se elimina de una prueba de confiabilidad antes de fallar, o una unidad que está en el campo y todavía está operando en el momento en que se determina la confiabilidad de estas unidades, se denomina elemento suspendido o censurado por la derecha observación o censurado a la derecha punto de datos . El análisis de artículos suspendidos también se consideraría cuando:

1. Necesitamos hacer un análisis de los resultados disponibles antes de completar la prueba.
2. Los modos de falla que están ocurriendo son diferentes a los previstos y dichas unidades se retiran de la prueba.
3. Necesitamos analizar un solo modo y el conjunto de datos real comprende múltiples modos.
4. Se análisis de garantía de todas las unidades en el campo (unidades no defectuosas y defectuosas). Las unidades no fallidas se consideran elementos suspendidos (o censurados por la derecha).

Esta sección describe los métodos de clasificación que se utilizan tanto en el gráfico de probabilidad como en los mínimos cuadrados (regresión de clasificación) para manejar datos censurados. Esto incluye:

• El método de ajuste de rango para datos censurados por la derecha (suspensión).
• El método de clasificación alternativo de ReliaSoft para datos censurados, incluidos datos censurados por la izquierda, censurados por la derecha e intervalos.

Método de ajuste de rango para datos censurados por la derecha

Cuando se utiliza el método de gráficos de probabilidad o de mínimos cuadrados (regresión de rango) para conjuntos de datos donde algunas de las unidades no fallaron o fueron suspendidas, necesitamos ajustar su probabilidad de falla o falta de confiabilidad. Como se discutió anteriormente, las estimaciones de la falta de confiabilidad de los datos completos se obtienen utilizando el enfoque de rangos medianos. La siguiente metodología ilustra cómo se calculan los rangos medianos ajustados para dar cuenta de los datos censurados por la derecha. Para ilustrar mejor la metodología, considere el siguiente ejemplo en Kececioglu [20] donde se prueban cinco elementos que dan como resultado tres fallas y dos suspensiones.

Número de artículo (Posición)	Fracaso (F) o Suspensión (S)	Vida útil del artículo, h
1	F 1	5,100
2	S 1	9,500
3	F 2	15,000
4	S 2	22,000
5	F3 _	40,000

La metodología para trazar elementos suspendidos implica ajustar las posiciones de clasificación y trazar los datos en función de las nuevas posiciones, determinadas por la ubicación de las suspensiones. Si consideramos estas cinco unidades, se utilizaría la siguiente metodología: El primer elemento debe ser la primera falla; por lo tanto, se le asigna el número de orden de falla j = 1 . El número de orden de falla real (o posición) de la segunda falla, F 2 está en duda Podría estar en la posición 2 o en la posición 3. Tenía S 1 no se ha retirado de la prueba a las 9.500 horas, podría haber funcionado con éxito pasadas las 15.000 horas, por lo que F 2 en la posición 2. Alternativamente, S 1 también podría haber fallado antes de las 15.000 horas, por lo que F 2 en la posición 3. En este caso, el número de orden de falla para F 2 será algún número entre 2 y 3. Para determinar este número, considere lo siguiente:

Podemos encontrar el número de formas en que puede ocurrir la segunda falla en el orden número 2 (posición 2) o en el orden número 3 (posición 3). Las formas posibles se enumeran a continuación.

F 2 en la posición 2						O	F 2 en la posición 3
1	2	3	4	5	6		1	2
F 1	F 1	F 1	F 1	F 1	F 1		F 1	F 1
F 2	F 2	F 2	F 2	F 2	F 2		S 1	S 1
S 1	S 2	F3 _	S 1	S 2	F3 _		F 2	F 2
S 2	S 1	S 1	F3 _	F3 _	S 2		S 2	F3 _
F3 _	F3 _	S 2	S 2	S 1	S 1		F3 _	S 2

Se puede ver que F 2 puede ocurrir en la segunda posición de seis maneras y en la tercera posición de dos maneras. La posición más probable es el promedio de estas formas posibles, o el número medio de orden ( MON ), dado por:

F 2 = METRO O N 2 = ( 6 x 2 ) + ( 2 x 3 ) 6 + 2 = 2.25

Siguiendo la misma lógica en el tercer fallo, se puede ubicar en las posiciones números 3, 4 y 5 de las posibles formas que se indican a continuación.

F3 _ en la posición 3		O	F3 _ en la posición 4			O	F3 _ en la posición 5
1	2		1	2	3		1	2	3
F 1	F 1		F 1	F 1 >	F 1		F 1	F 1	F 1
F 2	F 2		S 1	F 2	F 2		S 1	F 2	F 2
F3 _	F3 _		F 2	S 1	S 2		F 2	S 1	S 2
S 1	S 2		F3 _	F3 _	F3 _		S 2	S 2	S 1
S 2	S 1		S 2	S 2	S 1		F3 _	F3 _	F3 _

Entonces, el número de orden medio para la tercera falla (ítem 5) es:

METRO O N 3 = ( 2 x 3 ) + ( 3 x 4 ) + ( 3 x 5 ) 2 + 3 + 3 = 4.125

Una vez que se ha establecido el número de orden medio para cada falla, obtenemos las posiciones de rango medio para estas fallas en su número de orden medio. Específicamente, obtenemos el rango mediano de los números de orden 1, 2.25 y 4.125 de un tamaño de muestra de 5, como se indica a continuación.

Posiciones de trazado para las fallas (tamaño de muestra = 5)
Número de falla	MI	Posición de clasificación mediana (%)
1: F 1	1	13%
2: F 2	2.25	36%
3: F3 _	4.125	71%

Una vez que se han obtenido los valores del rango medio, el análisis del gráfico de probabilidad es idéntico al presentado anteriormente. Como habrás notado, esta metodología es bastante laboriosa. A lo largo de los años se han desarrollado otras técnicas y atajos para agilizar este procedimiento. Para obtener más detalles sobre este método, consulte Kececioglu [20] . Aquí, presentaremos uno de estos métodos. Este método calcula MON usando un incremento, I , que se define por:

yo yo = norte + 1 - PAGS METRO O N 1 + norte yo segundo PAGS S S

Donde

• N = el tamaño de la muestra o el número total de elementos en la prueba
• PMON = número de pedido medio anterior
• NIBPSS = el número de elementos más allá del conjunto suspendido actual. Es el número de unidades (incluyendo todas las fallas y suspensiones) en el tiempo de falla actual.
• i = el iésimo elemento de falla

MON se da como:

METRO O N yo = METRO O N yo - 1 + yo yo

Calculemos el ejemplo anterior usando el método.

Para F1:

METRO O N 1 = METRO O N 0 + yo 1 = 5 + 1 - 0 1 + 5 = 1

Para F2:

METRO O norte 2 = METRO O norte 1 + yo 2 = 1 + 5 + 1 - 1 1 + 3 = 2,25

Para F3:

METRO O N 3 = METRO O N 2 + yo 3 = 2,25 + 5 + 1 - 2,25 1 + 1 = 4,125

El MON obtenido para cada elemento de falla a través de este método es el mismo que el del primer método, por lo que los valores de rango mediano también serán los mismos.

Para datos agrupados, el incremento yo yo en cada grupo de fallas se multiplicará por el número de fallas en ese grupo.

Deficiencias del método de ajuste de rango

Aunque el método de ajuste de rango es el método más utilizado para realizar análisis de elementos suspendidos, nos gustaría señalar la siguiente deficiencia. Como habrás notado, solo se tiene en cuenta la posición donde ocurrió la falla, y no el tiempo exacto de suspensión. Por ejemplo, esta metodología produciría exactamente los mismos resultados para los próximos dos casos.

Caso 1			Caso 2
Número de artículo	Estado*"F" o "S"	Vida de un artículo, hr	Número de artículo	Estado*,"F" o "S"	Vida útil del artículo, h
1	F 1	1,000	1	F 1	1,000
2	S 1	1,100	2	S 1	9,700
3	S 2	1,200	3	S 2	9,800
4	S 3	1,300	4	S 3	9,900
5	F 2	10,000	5	F 2	10,000
* F - Reprobado, S - Suspendido			* F - Reprobado, S - Suspendido

Este déficit es significativo cuando el número de fallas es pequeño y el número de suspensiones es grande y no se distribuye uniformemente entre las fallas, como ocurre con estos datos. En casos como este, se recomienda encarecidamente utilizar la estimación de máxima verosimilitud (MLE) para estimar los parámetros en lugar de utilizar mínimos cuadrados, porque MLE no analiza los rangos ni las posiciones de trazado, sino que considera cada tiempo único hasta la falla o suspensión. . Para los datos dados anteriormente, los resultados son los siguientes. Los parámetros estimados utilizando el método recién descrito son los mismos para ambos casos (1 y 2):

β ˆˆ = η ˆˆ = 0 .81 11,400 h

Sin embargo, los resultados de MLE para el Caso 1 son:

β ˆˆ = η ˆˆ = 1,33 6.920 horas

Y los resultados de MLE para el Caso 2 son:

β ˆˆ = η ˆˆ = 0 .93 21,300 h

Como podemos ver, hay una diferencia considerable en los resultados de los dos conjuntos calculados usando MLE y los resultados usando la regresión con el SRM. Los resultados para ambos casos son idénticos cuando se utiliza la técnica de estimación de regresión con SRM, ya que SRM considera solo las posiciones de las suspensiones. Los resultados de MLE son bastante diferentes para los dos casos, con el segundo caso con un valor mucho mayor de la , lo que se debe a los valores más altos de los tiempos de suspensión en el Caso 2. Esto se debe a que la técnica de máxima verosimilitud, a diferencia de la regresión de rangos con SRM, considera los valores de las suspensiones al estimar los parámetros. Esto se ilustra en la discusión de MLE dada a continuación.

Una alternativa para mejorar el método de regresión es utilizar el siguiente método de clasificación de ReliaSoft (RRM) para calcular la clasificación. RRM sí considera el efecto del tiempo de censura.

Método de clasificación de ReliaSoft (RRM) para datos censurados por intervalos

Cuando se analizan datos de intervalo, es común suponer que el tiempo de falla real ocurrió en el punto medio del intervalo. Para ser más conservador, puede usar el punto inicial del intervalo o puede usar el punto final del intervalo para ser más optimista. Weibull++ le permite emplear el método de clasificación (RRM) de ReliaSoft al analizar datos de intervalo. Mediante un proceso iterativo, este método de clasificación es una mejora con respecto al método de clasificación estándar (SRM).

Al analizar datos censurados por la izquierda o la derecha, RRM también considera el efecto del tiempo de censura real. Por lo tanto, el rango resultante será más preciso que el SRM donde solo se usa la posición y no el tiempo exacto de censura.

Para obtener más detalles sobre este método, consulte Método de clasificación de ReliaSoft .

Estimación de máxima verosimilitud (MLE)

Desde un punto de vista estadístico, el método de estimación de máxima verosimilitud se considera, con algunas excepciones, como la más robusta de las técnicas de estimación de parámetros discutidas aquí. El método presentado en esta sección es para datos completos (es decir, datos que consisten solo en tiempos hasta la falla). El análisis de los datos censurados por la derecha (suspensión) y de los datos de intervalo o censurados por la izquierda se analizan en las siguientes secciones.

La idea básica detrás de MLE es obtener los valores más probables de los parámetros, para una distribución dada, que describirán mejor los datos. Como ejemplo, considere los siguientes datos (-3, 0, 4) y suponga que está tratando de estimar la media de los datos. Ahora, si tienes que elegir el valor más probable para la media entre -5, 1 y 10, ¿cuál elegirías? En este caso, el valor más probable es 1 (dado su límite de opciones). De manera similar, bajo MLE, uno determina los valores más probables para los parámetros de la distribución supuesta. Se formula matemáticamente de la siguiente manera.

Si X es una variable aleatoria continua con pdf :

F ( X ; θ 1 , θ 2 , ... , _ _ θ k )

donde θ 1 , θ 2 , _ . . , θ k son k parámetros desconocidos que necesitan ser estimados, con R observaciones independientes, X 1 , X 2 , ⋯ , X R , que corresponden en el caso de análisis de datos de vida a tiempos de falla. La función de verosimilitud está dada por:

L ( θ 1 , θ 2 , . . . , θ k | X 1 , X 2 , . . . , X R ) = L = ∏ R yo = 1 F ( X yo ; θ 1 , θ 2 , . . . , θ k )

yo = 1 , 2 , . . . , R

La función de verosimilitud logarítmica viene dada por:

Λ = en L = ∑ R yo = 1 en F ( X yo ; θ 1 , θ 2 , ... , _ _ Θ k )

Los estimadores de máxima verosimilitud (o valores de parámetros) de θ 1 , θ 2 , _ . . , θ k se obtienen maximizando L o Λ .

Al maximizar Λ con el que es mucho más fácil trabajar que con L , los estimadores de máxima verosimilitud (MLE) de θ 1 , θ 2 , _ . . , θ k son las soluciones simultáneas de k ecuaciones tales que:

∂ Λ ∂ θ j = 0 , j=1,2...,k

Aunque es una práctica común graficar las soluciones MLE usando rangos medianos (los puntos se grafican de acuerdo con los rangos medianos y la línea de acuerdo con las soluciones MLE), esto no es completamente representativo. Como se puede ver en las ecuaciones anteriores, el método MLE es independiente de cualquier tipo de rango. Por esta razón, la solución MLE a menudo parece no rastrear los datos en el gráfico de probabilidad. Esto es perfectamente aceptable porque los dos métodos son independientes entre sí y de ninguna manera sugiere que la solución sea incorrecta.

MLE para datos censurados por la derecha

Al realizar un análisis de máxima verosimilitud en datos con elementos suspendidos, la función de probabilidad debe expandirse para tener en cuenta los elementos suspendidos. La técnica general de estimación no cambia, pero se agrega otro término a la función de probabilidad para dar cuenta de los elementos suspendidos. Más allá de eso, el método para resolver las estimaciones de los parámetros sigue siendo el mismo. Por ejemplo, considere una distribución donde X es una variable aleatoria continua con pdf y cdf :

F ( X ; θ 1 , θ 2 , ... , _ _ θ k ) F ( X ; θ 1 , θ 2 , ... , _ _ θ k )

donde θ 1 , θ 2 , _ . . , θ k son los parámetros desconocidos que deben estimarse a partir de R fallas observadas en T 1 , T 2 , . . . , NIÑOS _ , y METRO suspensiones observadas en S 1 , S 2 , . . . , SM _ entonces la función de verosimilitud se formula de la siguiente manera:

L ( θ 1 , ... , _ _ Θ k | T 1 , ... , _ _ T R , S 1 , ... , _ _ S METRO ) = ∏ R yo = 1 F ( T yo ; θ 1 , θ 2 ,. _ . _ , θ k ) ⋅ ∏ METRO j = 1 [ 1 - F ( S j ; θ 1 , θ 2 , ... , _ _ θ k ) ]

Los parámetros se resuelven maximizando esta ecuación. En la mayoría de los casos, no existe una solución de forma cerrada para este máximo o para los parámetros. Las soluciones específicas para cada distribución que utiliza MLE se presentan en el Apéndice D.

MLE para intervalos y datos censurados a la izquierda

La inclusión de datos censurados por intervalos y por la izquierda en una solución MLE para estimaciones de parámetros implica agregar un término a la ecuación de probabilidad para tener en cuenta los tipos de datos en cuestión. Cuando se utilizan datos de intervalo, se supone que las fallas ocurrieron en un intervalo; es decir, en el intervalo desde el tiempo UN al tiempo B (o desde el momento 0 hasta el momento B si se deja censurado), donde A < B . En el caso de datos de intervalo, y dado PAG observaciones de intervalo, la función de verosimilitud se modifica multiplicando la función de verosimilitud con un término adicional de la siguiente manera:

L ( θ 1 , θ 2 , . . . , θ k | X 1 , X 2 , . . . , X PAGS ) = ∏ PAGS yo = 1 { F ( X yo ; θ 1 , θ 2 , . . . , θ k )   - F ( X yo - 1 ; θ 1 , θ 2 , . . . , θ k ) }

Tenga en cuenta que si solo están presentes datos de intervalo, este término representará la función de probabilidad completa para la solución MLE. La siguiente sección da una formulación de la función de verosimilitud completa para todos los esquemas de censura posibles.

La función de probabilidad completa

Ahora hemos visto que obtener estimaciones de parámetros MLE para diferentes tipos de datos implica incorporar diferentes términos en la función de probabilidad para dar cuenta de datos completos, datos censurados por la derecha y datos censurados por intervalos a la izquierda. Después de incluir los términos para los diferentes tipos de datos, la función de verosimilitud ahora se puede expresar en su forma completa o:

L = ∏ R yo = 1 F ( T yo ; θ 1 , ... , _ _ Θ k ) ⋅ ∏ METRO j = 1 [ 1 - F ( S j ; θ 1 , ... , _ _ Θ k ) ] ⋅ ∏ PAGS l = 1 { F ( yo l U ; θ 1 , ... , _ _ θ k ) - F ( yo l L ; θ 1 , ... , _ _ θ k ) }

donde:

L → L ( θ 1 , . . . , θ k | T 1 , . . . , T R , S 1 , . . . , S M , I 1 , . . . I P )

y:

• R es el número de unidades con fallas exactas
• METRO es el número de unidades suspendidas
• PAG es el número de unidades con censura a la izquierda o tiempos de intervalo hasta el fallo
• θk _ son los parámetros de la distribución
• _ Yo es el yo t h tiempo al fracaso
• s j es el j t h tiempo de suspensión
• yo _ tu es el final del intervalo de tiempo de l t h grupo
• Yo l L es el comienzo del intervalo de tiempo de l t h grupo

El número total de unidades es norte = R + M + P . Cabe señalar que en esta formulación, si R , METRO o PAG es cero, entonces se supone que el término del producto asociado con ellos es uno y no cero.

Comentarios sobre el método MLE

El método MLE tiene muchas propiedades de muestras grandes que lo hacen atractivo para su uso. Es asintóticamente consistente, lo que significa que a medida que aumenta el tamaño de la muestra, las estimaciones convergen a los valores correctos. Es asintóticamente eficiente, lo que significa que para muestras grandes, produce las estimaciones más precisas. Es asintóticamente imparcial, lo que significa que para muestras grandes, uno espera obtener el valor correcto en promedio. La distribución de las propias estimaciones es normal, si la muestra es lo suficientemente grande, y esta es la base para los límites de confianza habituales de la matriz de Fisher se analizan más adelante. Todas estas son excelentes propiedades para muestras grandes.

Desafortunadamente, el tamaño de la muestra necesaria para lograr estas propiedades puede ser bastante grande: de treinta a cincuenta a más de cien tiempos de falla exactos, dependiendo de la aplicación. Con menos puntos, los métodos pueden estar muy sesgados. Se sabe, por ejemplo, que las estimaciones MLE del parámetro de forma para la distribución de Weibull están muy sesgadas para tamaños de muestra pequeños, y el efecto puede incrementarse dependiendo de la cantidad de censura. Este sesgo puede causar importantes discrepancias en el análisis. También existen situaciones patológicas en las que no se aplican las propiedades asintóticas del MLE. Uno de ellos es estimar el parámetro de ubicación para la distribución de Weibull de tres parámetros cuando el parámetro de forma tiene un valor cercano a 1. Estos problemas también pueden causar discrepancias importantes.

Sin embargo, MLE puede manejar las suspensiones y los datos de intervalo mejor que la regresión de rango, particularmente cuando se trata de un conjunto de datos fuertemente censurado con pocos tiempos de falla exactos o cuando los tiempos de censura están distribuidos de manera desigual. También puede proporcionar estimaciones con una o ninguna falla observada, lo que la regresión de rangos no puede hacer. Como regla general, nuestra recomendación es utilizar técnicas de regresión de rangos cuando los tamaños de muestra son pequeños y sin censura intensa (la censura se analiza en Clasificaciones de datos de vida ). Cuando hay una censura fuerte o desigual, cuando hay una alta proporción de datos de intervalo y/o cuando el tamaño de la muestra es suficiente, se debe preferir MLE.

Ver también:

• Ejemplo de estimación de parámetros de máxima verosimilitud
• Análisis de datos agrupados

Métodos de estimación de parámetros bayesianos

Hasta este punto, nos hemos ocupado exclusivamente de lo que comúnmente se conoce como estadística clásica. En esta sección, se presentará otra escuela de pensamiento en el análisis estadístico, a saber, la estadística bayesiana. La premisa de las estadísticas bayesianas (dentro del contexto del análisis de datos de vida) es incorporar conocimientos previos, junto con un conjunto dado de observaciones actuales, para poder hacer inferencias estadísticas. La información previa podría provenir de datos operativos u observacionales, de experimentos previos comparables o de conocimientos de ingeniería. Este tipo de análisis puede ser particularmente útil cuando hay datos de prueba limitados para un diseño o modo de falla determinado, pero existe una sólida comprensión previa del comportamiento de la tasa de falla para ese diseño o modo. Al incorporar información previa sobre los parámetros, se puede obtener una distribución posterior para los parámetros y se pueden hacer inferencias sobre los parámetros del modelo y sus funciones. Esta sección pretende brindar una descripción general rápida y elemental de los métodos bayesianos, centrada principalmente en el material necesario para comprender los métodos de análisis bayesianos disponibles en Weibull++. Se puede encontrar una amplia cobertura del tema en numerosos libros que tratan sobre estadísticas bayesianas.

Regla de Bayes

La regla de Bayes proporciona el marco para combinar información previa con datos de muestra. En esta referencia, aplicamos la regla de Bayes para combinar información previa sobre los parámetros de la distribución supuesta con datos de muestra para hacer inferencias basadas en el modelo. El conocimiento previo sobre el(los) parámetro(s) se expresa en términos de φ ( θ ) , llamada distribución previa . La posterior distribución θ dados los datos de la muestra, utilizando la regla de Bayes, proporciona la información actualizada sobre los parámetros θ . Esto se expresa con el siguiente pdf :

F ( θ | re un t un ) = L ( re un t un | θ ) φ ( θ ) ∫ ζ L ( re un t un | θ ) φ ( θ ) re ( θ )

donde:

• θ es un vector de los parámetros de la distribución elegida
• gramo es el rango de θ
• L ( D a t a | θ ) es la función de verosimilitud basada en la distribución y los datos elegidos
• φ ( θ ) es la distribución previa para cada uno de los parámetros

La integral en la ecuación de la regla de Bayes a menudo se denomina probabilidad marginal, que es un número constante que se puede interpretar como la probabilidad de obtener los datos de la muestra dada una distribución previa. Generalmente, la integral en la ecuación de la regla de Bayes no tiene una solución de forma cerrada y se necesitan métodos numéricos para su solución.

Como se puede ver en la ecuación de la regla de Bayes, existe una diferencia significativa entre las estadísticas clásicas y bayesianas. Primero, la idea de información previa no existe en la estadística clásica. Todas las inferencias en la estadística clásica se basan en los datos de la muestra. Por otro lado, en el marco bayesiano, la información previa constituye la base de la teoría. Otra diferencia está en el enfoque general de hacer inferencias y su interpretación. Por ejemplo, en el análisis bayesiano, los parámetros de la distribución a ajustar son las variables aleatorias. En realidad, no hay una distribución ajustada a los datos en el caso bayesiano.

Por ejemplo, considere el caso en que los datos se obtienen de una prueba de confiabilidad. Con base en la experiencia previa con un producto similar, el analista cree que el parámetro de forma de la distribución de Weibull tiene un valor entre 1 _ y β2 _ y quiere utilizar esta información. Esto se puede lograr usando el teorema de Bayes. En este punto, el analista está forzando automáticamente la distribución de Weibull como modelo para los datos y con un parámetro de forma entre 1 _ y β2 _ . En este ejemplo, el rango de valores para el parámetro de forma es la distribución anterior, que en este caso es Uniforme. Aplicando la regla de Bayes se obtendrá la distribución posterior del parámetro de forma. Por lo tanto, terminamos con una distribución del parámetro en lugar de una estimación del parámetro, como en la estadística clásica.

Para ilustrar mejor el ejemplo, suponga que se proporcionó un conjunto de datos de fallas junto con una distribución para el parámetro de forma (es decir, anterior uniforme) del Weibull (suponiendo automáticamente que los datos tienen una distribución de Weibull). En base a eso, se obtiene una nueva distribución (la posterior) para ese parámetro usando la regla de Bayes. Esta distribución posterior del parámetro puede o no parecerse en forma a la distribución previa supuesta. En otras palabras, en este ejemplo la distribución previa de b se asumió que era uniforme, pero lo más probable es que la parte posterior no tenga una distribución uniforme.

La pregunta ahora es: ¿cuál es el valor del parámetro de forma? ¿Qué pasa con la confiabilidad y otros resultados de interés? Para responder a estas preguntas, debemos recordar que en el marco bayesiano todas estas métricas son variables aleatorias. Por lo tanto, para obtener una estimación, se debe especificar una probabilidad o podemos usar el valor esperado de la distribución posterior.

Para demostrar el procedimiento de obtención de resultados a partir de la distribución posterior, reescribiremos la ecuación de la regla de Bayes para un solo parámetro θ 1 :

F ( θ | re un t un ) = L ( re un t un | θ 1 ) φ ( θ 1 ) ∫ ζ L ( re un t un | θ 1 ) φ ( θ 1 ) re ( θ )

El valor esperado (o valor medio) del parámetro θ 1 se puede obtener usando la ecuación para la media y la ecuación de la regla de Bayes para un solo parámetro:

mi ( θ 1 ) = metro θ 1 = ∫ ζ θ 1 ⋅ F ( θ 1 | re un t un ) re θ 1

Un resultado alternativo para θ 1 sería el valor de la mediana. Usando la ecuación para la mediana y la ecuación de la regla de Bayes para un solo parámetro:

∫ θ 0.5 - ∞ , 0 F ( θ 1 | re un t un ) re θ 1 = 0.5

La ecuación de la mediana se resuelve para θ 0.5 el valor medio de θ 1

cualquier otro percentil de la función de densidad de probabilidad posterior . se puede calcular e informar Por ejemplo, se podría calcular el percentil 90 de θ 1 ’s posterior pdf :

∫ θ 0.9 - ∞ , 0 F ( θ 1 | re un t un ) re θ 1 = 0.9

Este cálculo se utilizará en límites de confianza y la distribución de Weibull para obtener límites de confianza en los parámetros.

El siguiente paso será hacer inferencias sobre la confiabilidad. Dado que el parámetro θ 1 es una variable aleatoria descrita por la probabilidad posterior, todas las funciones subsiguientes de θ 1 también son variables aleatorias distribuidas y se basan completamente en la función de densidad probabilidad de θ 1 . Por lo tanto, también será necesario calcular el valor esperado, la mediana u otros valores percentiles. Por ejemplo, la confiabilidad esperada en el tiempo T es:

mi [ R ( T | re un t un ) ] = ∫ ς R ( T ) F ( θ | re un t un ) re θ

En otras palabras, en un momento dado T , existe una distribución que gobierna el valor de confiabilidad en ese momento, T , y usando la regla de Bayes se obtiene el valor esperado (o medio) de la confiabilidad. También se pueden obtener otros percentiles de esta distribución. Se sigue un procedimiento similar para otras funciones de θ 1 , como la tasa de fallas, la vida confiable, etc.

Distribuciones anteriores

Las distribuciones anteriores juegan un papel muy importante en las estadísticas bayesianas. Son esencialmente la base del análisis bayesiano. Existen diferentes tipos de distribuciones previas, a saber, informativas y no informativas . Las distribuciones previas no informativas (también conocidas como vagas , planas y difusas ) son distribuciones que no tienen una base poblacional y juegan un papel mínimo en la distribución posterior. La idea detrás del uso de distribuciones previas no informativas es hacer inferencias que no se vean muy afectadas por la información externa o cuando la información externa no esté disponible. La distribución uniforme se utiliza con frecuencia como un dato previo no informativo.

Por otro lado, los previos informativos tienen una mayor influencia en la distribución posterior. La influencia de la distribución previa sobre la posterior está relacionada con el tamaño de la muestra de los datos y la forma de la anterior. En términos generales, se requieren tamaños de muestra grandes para modificar los datos previos fuertes, mientras que los datos previos débiles se ven abrumados incluso por tamaños de muestra relativamente pequeños. Los antecedentes informativos generalmente se obtienen de datos pasados.