ReliaWiki, Estimacion de parametros de confiabilidad por el metodo de minimos cuadrados.

 

Mínimos cuadrados (regresión de rangos)

Utilizando la idea del gráfico de probabilidad, el análisis de regresión ajusta matemáticamente la mejor línea recta a un conjunto de puntos, en un intento de estimar los parámetros. Esencialmente, esta es una versión matemática del método de trazado de probabilidades discutido anteriormente.

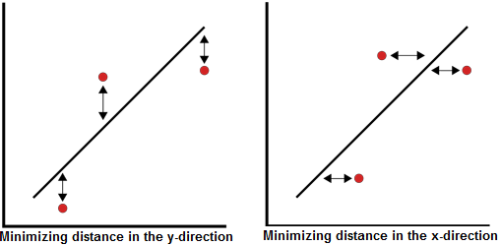
El método de mínimos cuadrados lineales se utiliza para todos los análisis de regresión realizados por Weibull++, excepto en los casos de las distribuciones Weibull de 3 parámetros, Weibull mixta, gamma y gamma generalizada, donde se emplea una técnica de regresión no lineal. los términos regresión lineal y mínimos cuadrados En esta referencia se utilizan como sinónimos En Weibull++, el término La regresión de rango se utiliza en lugar de mínimos cuadrados o regresión lineal, porque la regresión se realiza en los valores de rango, más específicamente, los valores de rango mediano (representados en el eje y). El método de mínimos cuadrados requiere que se ajuste una línea recta a un conjunto de puntos de datos, de modo que se minimice la suma de los cuadrados de la distancia de los puntos a la línea ajustada. Esta minimización se puede realizar en dirección vertical u horizontal. Si la regresión está en , luego la línea se ajusta de manera que se minimicen las desviaciones horizontales de los puntos a la línea. Si la regresión es en Y, entonces esto significa que la distancia de las desviaciones verticales desde los puntos a la recta se minimiza. Esto se ilustra en la siguiente figura.

Regresión de rango en Y

Supongamos que un conjunto de pares de datos , ,..., fueron obtenidos y trazados, y que el -Los valores se conocen exactamente. Entonces, según el principio de mínimos cuadrados, que minimiza la distancia vertical entre los puntos de datos y la línea recta ajustada a los datos, la línea recta que mejor se ajusta a estos datos es la línea recta (donde el recientemente introducido ( ) el símbolo indica que este valor es una estimación) tal que:

y donde y son los estimaciones de mínimos cuadrados de y , y es el número de puntos de datos. Estas ecuaciones se minimizan mediante estimaciones de y tal que:

y:

Regresión de rango en X

Supongamos que un conjunto de pares de datos... ,..., se obtuvieron y representaron, y que los valores de y se conocen exactamente. Se aplica el mismo principio de mínimos cuadrados, pero esta vez minimizando la distancia horizontal entre los puntos de datos y la línea recta ajustada a los datos. La línea recta que mejor se ajusta a estos datos es la línea recta tal que:

De nuevo, y son las estimaciones de mínimos cuadrados de y , y es el número de puntos de datos. Estas ecuaciones se minimizan mediante estimaciones de y tal que:

y:

Las relaciones correspondientes para determinar los parámetros de distribuciones específicas (es decir, Weibull, exponencial, etc.) se presentan en los capítulos que cubren esa distribución. 

Coeficiente de correlación

El coeficiente de correlación es una medida de qué tan bien se ajusta el modelo de regresión lineal a los datos y generalmente se denota por . En el caso del análisis de datos de vida, es una medida de la fuerza de la relación lineal (correlación) entre los rangos medianos y los datos. El coeficiente de correlación poblacional se define de la siguiente manera:

dónde covarianza de y , desviación estándar de , y desviación estándar de .

El estimador de es el coeficiente de correlación muestral, , dado por:

el rango de es .

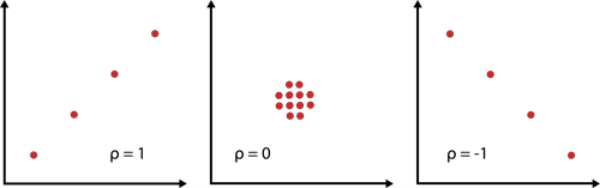
Cuanto más se acerque el valor a , mejor será el ajuste lineal. Tenga en cuenta que +1 indica un ajuste perfecto (los valores emparejados ( ) se encuentran en una línea recta) con pendiente positiva, mientras que -1 indica un ajuste perfecto con pendiente negativa. Un valor del coeficiente de correlación de cero indicaría que los datos están dispersos aleatoriamente y no tienen ningún patrón o correlación en relación con el modelo de línea de regresión.

Comentarios sobre el método de los mínimos cuadrados

El método de estimación de mínimos cuadrados es bastante bueno para funciones que pueden linealizarse. Para estas distribuciones, los cálculos son relativamente fáciles y directos, y tienen soluciones de forma cerrada que pueden arrojar fácilmente una respuesta sin tener que recurrir a técnicas numéricas o tablas. Además, esta técnica proporciona una buena medida de la bondad de ajuste de la distribución elegida en el coeficiente de correlación. Los mínimos cuadrados generalmente se utilizan mejor con conjuntos de datos que contienen datos completos, es decir, datos que consisten únicamente en tiempos únicos hasta el fallo sin datos censurados o de intervalo. (Ver Clasificación de datos de vida para obtener información sobre los diferentes tipos de datos, incluidos datos completos, censurados por la izquierda, censurados por la derecha (o suspendidos) y de intervalo).