domingo, 17 de mayo de 2009

Mecánica de fluidos

De Wikipedia, la enciclopedia libre

(Redirigido desde Dinámica de fluidos)
Perturbación provocada por un avión al despegar hecha visible con humo coloreado.

La mecánica de fluidos es la rama de la mecánica de medios continuos (que a su vez es una rama de la física) que estudia el movimiento de los fluidos (gases y líquidos) así como las fuerzasfluidos es su incapacidad para resistir esfuerzos cortantes (lo que provoca que carezcan de forma definida). También estudia las interacciones entre el fluido y el contorno que lo limita. La hipótesis fundamental en la que se basa toda la mecánica de fluidos es la hipótesis del medio continuo. que los provocan. La característica fundamental que define a los

Contenido

[ocultar]

Hipótesis básicas [editar]

Como en todas las ramas de la física, en la mecánica de fluidos se parte de unas hipótesis a partir de las cuales se desarrollan todos los conceptos. En particular, en la mecánica de fluidos se asume que los fluidos verifican las siguientes leyes: -Conservación de la masa y de la cantidad de movimiento -Primera y segunda ley de la termodinámica Pero probablemente la hipótesis más importante de la mecánica de fluidos es la hipótesis del medio continuo.

Hipótesis del medio continuo [editar]

La hipótesis del medio continuo es la hipótesis fundamental de la mecánica de fluidos y en general de toda la mecánica de medios continuos. En esta hipótesis se considera que el fluido es continuo a lo largo del espacio que ocupa, ignorando por tanto su estructura molecular y las discontinuidades asociadas a esta. Con esta hipótesis se puede considerar que las propiedades del fluido (densidad, temperatura, etc.) son funciones continuas.

La forma de determinar la validez de esta hipótesis consiste en comparar el camino libre medio de las moléculas con la longitud característica del sistema físico. Al cociente entre estas longitudes se le denomina número de Knudsen. Cuando este número adimensional es mucho menor a la unidad, el material en cuestión puede considerarse un fluido (medio continuo). En el caso contrario los efectos debidos a la naturaleza molecular de la materia no pueden ser despreciados y debe utilizarse la mecánica estadística para predecir el comportamiento de la materia.(Ejemplos de situaciones donde la hipótesis del medio continuo no es válida pueden encontrarse en el estudio de los plasmas.

Concepto de partícula fluida [editar]

Este concepto esta muy ligado al del medio continuo y es sumamente importante en la mecánica de fluidos. Se llama partícula fluida a la masa elemental de fluido que en un instante determinado se encuentra en un punto del espacio. Dicha masa elemental ha de ser lo suficientemente grande como para contener un gran número de moléculas, y lo suficientemente pequeña como para poder considerar que en su interior no hay variaciones de las propiedades macroscópicas del fluido, de modo que en cada partícula fluida podamos asignar un valor a estas propiedades. Es importante tener en cuenta que la partícula fluida se mueve con la velocidad macroscópica del fluido, de modo que está siempre formada por las mismas moléculas. Así pues un determinado punto del espacio en distintos instantes de tiempo estará ocupado por distintas partículas fluidas.

Descripciones lagrangiana y euleriana del movimiento de un fluido[editar]

A la hora de describir el movimiento de un fluido existen dos puntos de vista. Una primera forma de hacerlo es seguir a cada partícula fluida en su movimiento, de manera que buscaremos unas funciones que nos den la posición, así como las propiedades de la partícula fluida en cada instante. Ésta es la descripción Lagrangiana. Una segunda forma es asignar a cada punto del espacio y en cada instante un valor para las propiedades o magnitudes fluidas sin importar la partícula fluida que en dicho instante ocupa ese punto. Ésta es la descripción Euleriana, que no está ligada a las partículas fluidas sino a los puntos del espacio ocupados por el fluido. En esta descripción el valor de una propiedad en un punto y en un instante determinado es el de la partícula fluida que ocupa dicho punto en ese instante.

La descripción euleriana es la usada comúnmente, puesto que en la mayoría de casos y aplicaciones es más útil. Usaremos dicha descripción para la obtención de las ecuaciones generales de la mecánica de fluidos.

Ecuaciones generales de la mecánica de fluidos [editar]

Artículo principal: Ecuaciones de Navier-Stokes

Las ecuaciones que rigen toda la mecánica de fluidos se obtienen por la aplicación de los principios de conservación de la mecánica y la termodinámica a un volumen fluido. Para generalizarlas usaremos el teorema del transporte de Reynolds y el teorema de la divergencia (o teorema de Gauss) para obtener las ecuaciones en una forma más útil para la formulación euleriana.

Las tres ecuaciones fundamentales son: la ecuación de continuidad, la ecuación de la cantidad de movimiento, y la ecuación de la conservación de la energía. Estas ecuaciones pueden darse en su formulación integral o en su forma diferencial, dependiendo del problema. A este conjunto de ecuaciones dadas en su forma diferencial también se le denomina ecuaciones de Navier-Stokes.

No existe una solución general a dicho conjunto de ecuaciones debido a su complejidad, por lo que para cada problema concreto de la mecánica de fluidos se estudian estas ecuaciones buscando simplificaciones que faciliten la resolución del problema. En algunos casos no es posible obtener una solución analítica, por lo que hemos de recurrir a soluciones numéricas generadas por ordenador. A esta rama de la mecánica de fluidos se la denomina mecánica de fluidos computacional.

Las ecuaciones son las siguientes:

Ecuación de continuidad:

-Forma integral: \frac{d}{dt}\int_{\Omega} \rho \; d\Omega = -\int_{\partial\Omega} \rho\mathbf{v\cdot n} d\partial\Omega

-Forma diferencial: \frac{\partial \rho}{\partial t} + \nabla\cdot\left(\rho\mathbf{v}\right) = 0

Ecuación de cantidad de movimiento:

-Forma integral: \frac{d}{dt}\int_{\Omega} \rho\mathbf{v} \; d\Omega +\int_{\partial\Omega} \rho\mathbf{v}\mathbf{v\cdot n} d\partial\Omega= \int_{\partial\Omega} \tau\mathbf{\cdot n} d\partial\Omega+ \int_{\Omega} \rho\mathbf{f} d\Omega

-Forma diferencial: 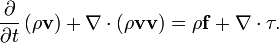\frac{\partial}{\partial t}\left(\rho \mathbf{v} \right) + \nabla \cdot (\rho \mathbf{v} \mathbf{v}) = \rho \mathbf{f}+\nabla \cdot \tau.

Ecuación de la energía

-Forma integral: \frac{d}{dt}\int_{\Omega} \rho\left (e+\frac {1}{2}v^2\right)\; d\Omega+\int_{\partial\Omega} \rho\left (e+\frac {1}{2}v^2\right)\mathbf{v\cdot n} d\partial\Omega=\int_{\partial\Omega} \mathbf{n}\cdot\tau\cdot\mathbf{v} \; d\partial\Omega+\int_{\Omega} \rho\mathbf{f\cdot v} \;d\Omega-\int_{\partial\Omega} \mathbf {q \cdot n} \; d\partial\Omega

-Forma diferencial: \rho\frac {D}{Dt}\left(e+\frac {1}{2}v^2 \right )=-\nabla\cdot\left(p\mathbf{v}\right)+\nabla\cdot\left(\tau'\cdot\mathbf{v}\right)+ \rho\mathbf{f\cdot v}+\nabla\cdot\left(k\nabla T\right)

Para un desarrollo más profundo de estas ecuaciones ver el artículo ecuaciones de Navier-Stokes

Véase también [editar]

Campos de estudio:

Ecuaciones matemáticas que describen el comportamiento de los fluidos:

Tipos de fluidos:

Tipos de flujo:

Propiedades de los fluidos:

Números adimensionales:

Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)